…
案例介绍
我们有一个变量是电影因素, 包括三个水平(情感意象/认知意象/故事情节), 并且还想考虑性别作为组间变量, 考察不同性别受各种电影因素的吸引力, 因为电影因素是组内设计, 也就是说每个被试都测量了情感意象/认知意象/故事情节这三个变量, 因此这种设计就叫做混合设计。
前提
- 因变量为连续变量
- 没有极端值
- 球形检验
- 各变量在各组内正态
- 组间方差齐性
SPSS操作
在菜单依次打开: 分析–>一般线性模型–>重复测量
重复测量需要定义组内因子, 所谓组内因子就是我们今天案例中讲的影响是否看某个电影的因素, 我们可以起名字为”电影因素”, 其中包含三种变量: 情感意象, 认知意象和故事情节, 所以级别数是3, 然后点击”添加”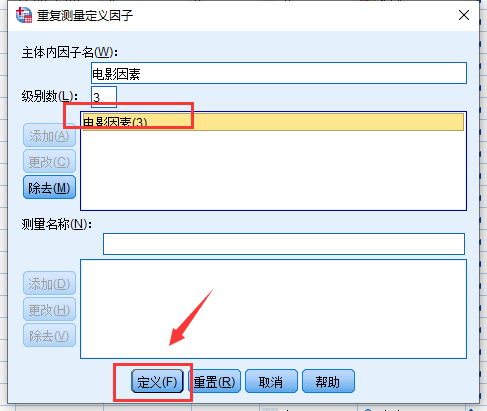
选择三个变量”情感意象, 认知意象和故事情节”为我们定义的因子的三个变量, 情感状态作为被试间因子: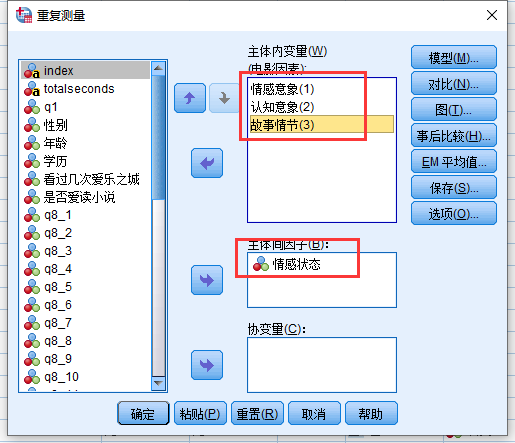
在”选项”对话框中, 我们需要勾选”描述统计”, “效应量估算”, “齐性检验”
在”EM平均值”对话框中, 我们将”情感状态x电影因素”这一项放入右侧的变量框中
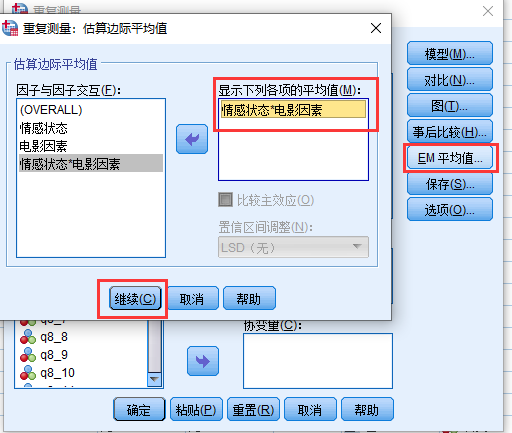
另外我们想要做一个折线图来显示各组均值, 所以我们在”图”对话框中, 按如下设置:
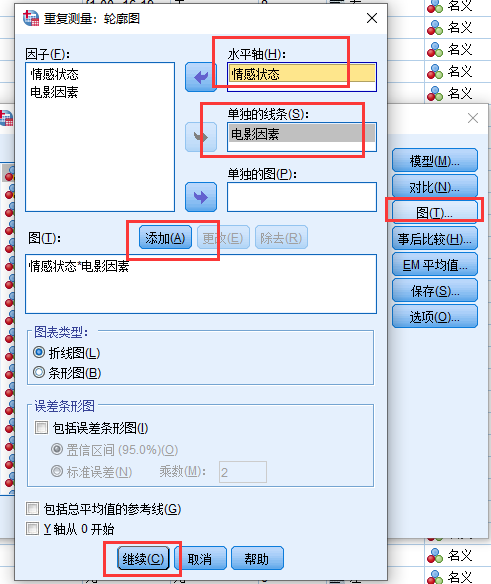
最后, 我们不是直接运行, 而是点击’粘贴”, 将代码粘贴到编辑器中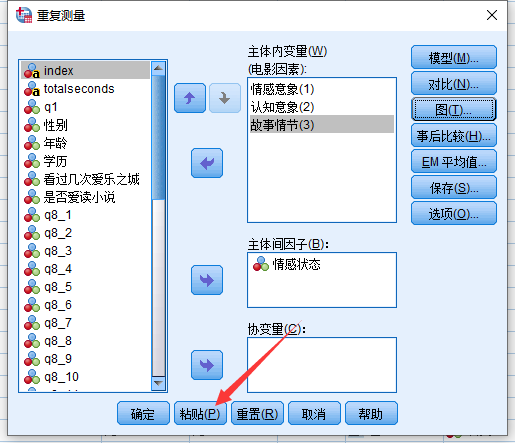
在这里, 我们需要将/EMMEANS这一行改成如下红框中所示, 这句代码就是为了进行简单效应分析, 也就是在不同的情感状态下比较不同的电影因素是否有均值差异。

结果解读
首先需要查看球形检验的结果, 如果显著性<0.05, 就认为数据不满足球星假设, 那么就需要对结果进行矫正, 否则不需要纠正。
我们的表格显示不符合球星假设,在实际应用中,只用Greenhouse-Geisser和Huynh-Feldt两种方法,这两种方法计算的epsilon (ε)的值越低,说明违反球形假设的程度越大,当epsilon=1时数据服从球形假设。 Maxwell & Delaney (2004)建议当epsilon<0.75时,使用Greenhouse-Geisser方法校正。其他统计学家建议当epsilon>0.75时,使用Huynh-Feldt方法。因此我们可以使用Huynh-Feldt方法。

方差齐性检验, 不管基于什么方法, 显著性都超过0.05, 因此可以认为组间方差差异不明显。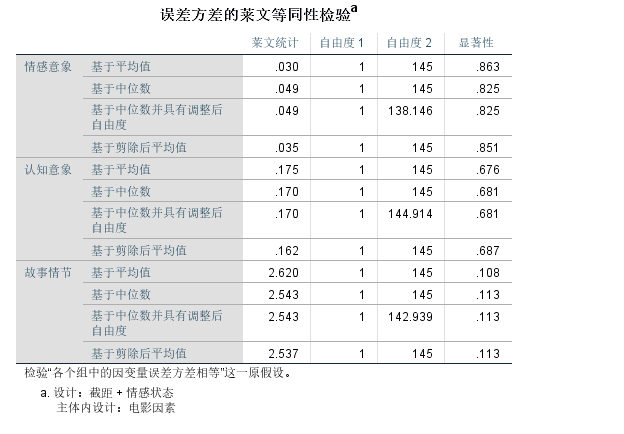
根据上面球形检验的结果, 我们需要采纳Huynh-Feldt的方法所得结果, 也就是下面红框中的结果: 电影因素的主效应显著F(1.814, 263)=6.177, p<.01。因此我们需要进行成对比较来确定具体哪些因素是有差异的。
由于”电影因素*情感状态”的交互效应显著F(1.814, 263)=9.431, p<.01, 因此我们需要进行简单效应分析。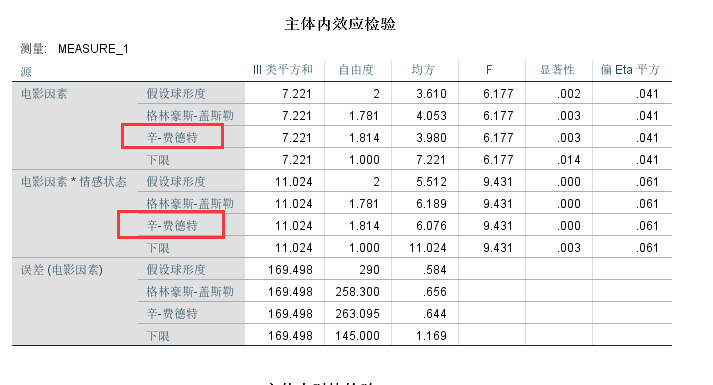
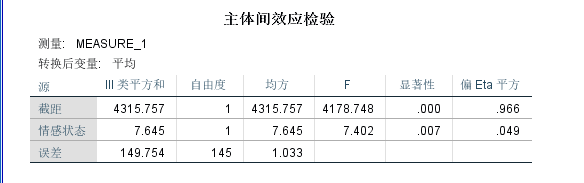
组间效应主要是指”情感状态”是否影响”电影因素”的三个指标的均值, 结果显示”情感状态”的主效应显著F(1, 145)=7.402, p<0.01。
交互作用显著, 我们进一步需要比较在不同情感状态下, 三个电影因素是否有差异。由于多重比较会提高犯错的概率, 因此我们需要降低显著性的标准, 通常是0.05除以比较的次数, 0.05/6=0.008, 因此以0.008为标准判断显著性, 低于0.008才认为显著。
在单身状态下, 故事情节(3)要显著低于情感意象(p=0.001)和和认知意象(p=0.007), 但是在婚恋状态下, 故事情节和情感意象没有显著差异, 但是故事情节却显著高于认知意象(p=0.001)。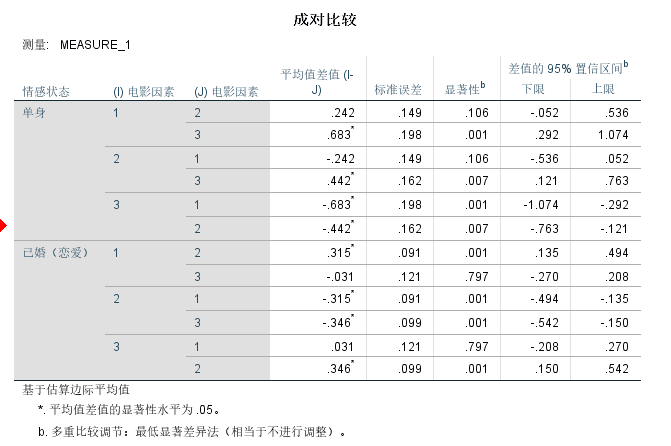
我们从折线图中更容易看清楚:
结论撰写
首先对组间变量”情感状态”进行组间的方差齐性检验, 结果显示方差差异不显著(L(1, 145)=0.3, p>0.05)。然后进行球形检验, 结果显著, 数据不满足球形假设($\lambda^2$
注意
本文由jupyter notebook转换而来, 您可以在这里下载notebook
统计咨询请加QQ 2726725926, 微信 mllncn, SPSS统计咨询是收费的
微博上@mlln-cn可以向我免费题问
请记住我的网址: mlln.cn 或者 jupyter.cn


